Height and Distance Questions Answers

• 1. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30 degree and 45 degree respectively. If the lighthouse is 100 m high, the distance between the two ships is:

  1. 276 metre
  2. 273 metre
  3. 270 metre
  4. 263 metre

  Answer And Explanation

  Answer: Option B

  

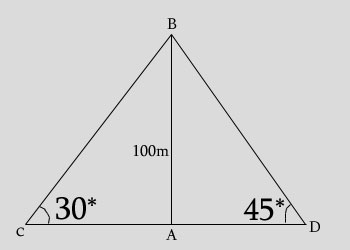
  Explanation:

  Let AB be the lighthouse and C and D be the positions of the ships.
  \begin{aligned}
  \text{AB = 100m}, \angle{ACB}=30^{\circ}, \\
  \angle{ADB}=45^{\circ}\\
  \frac{AB}{AC} = tan&30{\circ} = \frac{1}{\sqrt{3}} \\
  => AC = AB*\sqrt{3} = 100\sqrt{3}m\\
  
  \frac{AB}{AD} = tan&45^{\circ} = 1 \\
  => AB = AD = 100m\\
  
  CD = AC+AD\\
  = (100\sqrt{3}+100)&m \\
  = 100(\sqrt{3}+1)&m\\
  = 100*2.73&m
  = 273m
  
  \end{aligned}

  • View Answer
  • Comment on this question

• 2. The angle of elevation of the sun, when the length of the shadow of a tree is \begin{aligned}\sqrt{3}\end{aligned} times the height of tree, is :

  1. 30 degree
  2. 45 degree
  3. 60 degree
  4. 9 degree

  Answer And Explanation

  Answer: Option A

  

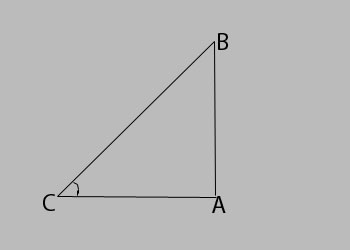
  Explanation:

  Let AB be the tree and AC be its shadow, So as per question, shadow of a tree is \begin{aligned}\sqrt{3}\end{aligned} times the height of tree. Let h be the height of the tree, then
  \begin{aligned}
  \frac{AB}{AC} = tan\theta \\
  => \frac{h}{\sqrt{3}h} = tan\theta \\
  => tan\theta = \frac{1}{\sqrt{3}} \\
  => \theta = 30^{\circ}
  \end{aligned}

  • View Answer
  • Comment on this question

• 3. From a point C on a level ground, the angle of elevation of the top of a tower is 30 degree. If the tower is 100 meter high, find the distance from point C to the foot of the tower.

  1. 170 meter
  2. 172 meter
  3. 173 meter
  4. 167 meter

  Answer And Explanation

  Answer: Option C

  

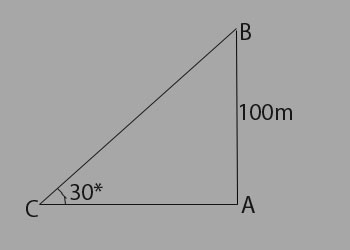
  Explanation:

  Let AB be the tower.
  \begin{aligned}
  then \angle{ACB}= 30^{\circ} \\
  AB = 100&meter \\
  \frac{AB}{AC} = tan&30^{\circ} \\
  =>\frac{100}{AC} = \frac{1}{\sqrt{3}} \\
  => AC = \sqrt{3}*100 \\
  => AC = 1.73*100 \\
  => AC = 173 meter
  \end{aligned}
  
  Please always remember the value of square root 3 is 1.73, and value of square root 2 is 1.41.
  This will be very helpful while solving height and distance questions and saving your time.

  • View Answer
  • Comment on this question

• 4. A man standing at a point C is watching the top of a tower, which makes an angle of elevation of 30 degree. The man walks some distance towards the tower to watch its top and the angle of elevation become 60 degree. What is the distance between the base of the tower and point C.

  1. \begin{aligned} 4\sqrt{3} meter \end{aligned}
  2. \begin{aligned} 2\sqrt{3} meter \end{aligned}
  3. \begin{aligned} \sqrt{3} meter \end{aligned}
  4. Data is inadequate

  Answer And Explanation

  Answer: Option D

  

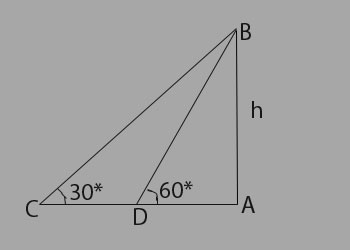
  Explanation:

  Please refer to the image. One of the AB, AD and CD must be given. So data is inadequate.

  • View Answer
  • Comment on this question

• 5. A man is watching form the top of the tower a boat speeding away from the tower. The boat makes the angle of depression of 45 degree with the man's eye when at a distance of 60 metres from the tower. After 5 seconds the angle of depression becomes 30 degree. What is the approximate speed of the boat, assuming that it is running in still water ?

  1. 22 Km/Hr
  2. 28 Km/Hr
  3. 32 Km/Hr
  4. 36 Km/Hr

  Answer And Explanation

  Answer: Option C

  

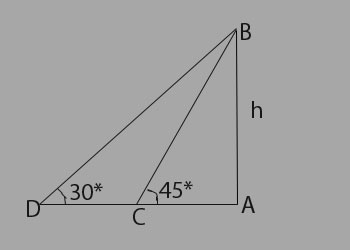
  Explanation:

  Let AB be the tower and C and D be the positions of the boat.
  \begin{aligned}
  then \angle{ACB}=45^{\circ}, \angle{ADB}=30^{\circ}, \\
  AC = 60&m \\
  Let& AB = h \\
  =>\frac{AB}{AC} = tan&45^{\circ} = 1 \\
  => AB = AC = 60&m \\
  
  and, \frac{AB}{AD} = tan&30^{\circ} = \frac{1}{\sqrt{3}} \\
  => AD = AB*\sqrt{3} = 60\sqrt{3}&m \\
  
  => CD = AD-AC = 60\sqrt{3}-60\\
  => CD = 60(\sqrt{3}-1) m \\
  \text{We Know Speed = }\frac{Distance}{Time} \\
  => Speed = \left[\frac{60(\sqrt{3}-1)}{5} \right]m/sec
  = 12*0.73&m/sec \\
  
  \text{Please note answer we need in Km/Hr} \\
  => Speed = 12*0.73*\frac{18}{5} Km/Hr \\
  => Speed = 31.5 & Km/hr, \\
  \text{Which is approx 32 Km/Hr}
  
  
  \end{aligned}

  • View Answer
  • Comment on this question

• 6. The Top of a 15 metre high tower makes an angle of elevation of 60 degree with the bottom of an electric pole and angle of elevation of 30 degree with the top of pole. Find the height of the electric pole.

  1. 7 metre
  2. 8 metre
  3. 9 metre
  4. 10 metre

  Answer And Explanation

  Answer: Option D

  

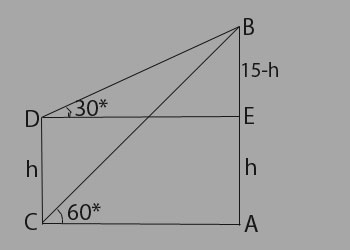
  Explanation:

  Let AB be the tower and CD be the electric pole.
  
  \begin{aligned}
  \angle{ACB}=60^{\circ}, \angle{EDB}=30^{\circ}, \\
  AB = 15&m \\
  Let & CD = h, \text{ then}, \\
  BE = AB-AE = AB - AE = 15-h\\
  \frac{AB}{AC} = tan 60^{\circ} = \sqrt{3} \\
  => AC = \frac{AB}{\sqrt{3}} \\
  => AC = \frac{15}{\sqrt{3}} \\
  and, & \frac{BE}{DE} = tan 30^{\circ} = \frac{1}{\sqrt{3}} \\
  => DE = (BE*\sqrt{3}) \\
  = \sqrt{3}(15-h) \\
  
  Now, & AC = DE \\
  => \frac{15}{\sqrt{3}} = \sqrt{3}(15-h) \\
  => 3h = 45-15 \\
  => h = \frac{30}{3} = 10 m
  \end{aligned}

  • View Answer
  • Comment on this question

• 7. A toy leaves the earth at a point A and rises vertically at uniform speed. After two minutes of vertical rise boy finds the angular elevation of the balloon as 60°.
  If the point at which boy is standing is 150 m away from point A, what is the speed of the toy ?

  1. .98 meter/second
  2. 1.08 meter/second
  3. 1.16 meter/second
  4. 2.08 meter/second
  5. 2.16 meter/second

  Answer And Explanation

  Answer: Option E

  

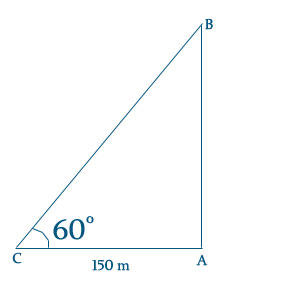
  Explanation:

  Let boy is standing at C position and A is that position from where toy left eartg and B is the position of the toy after 2 minutes.
  
  \begin{aligned}
  \text{ Given that CA = 150 m } \\
  \text{Angle is }\angle{ 60 ^{\circ} } \\
  tan 60 ^{\circ} = \frac{BA}{CA} \\
  BA = 150 \sqrt{3}
  \end{aligned}
  So distance travelled by toy is,
  \begin{aligned}
  150 \sqrt{3} \\
  \text { Total time taken is = 2 min} \\
  = \text {2 * 60 = 120 seconds } \\
  Speed = \frac{Distance}{Time} \\
  = \frac{150\sqrt{3}}{120} = 1.25\sqrt{3}\\
  = \text {1.25 * 1.73 = 2.16 mtr/sec}
  \end{aligned}
  
  

  • View Answer
  • Comment on this question